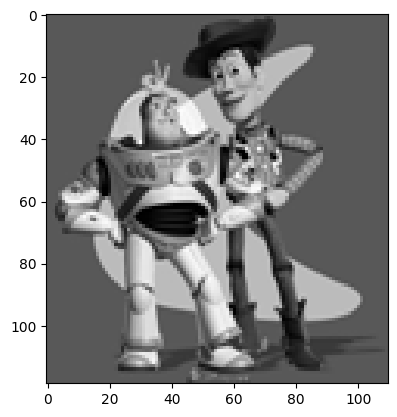
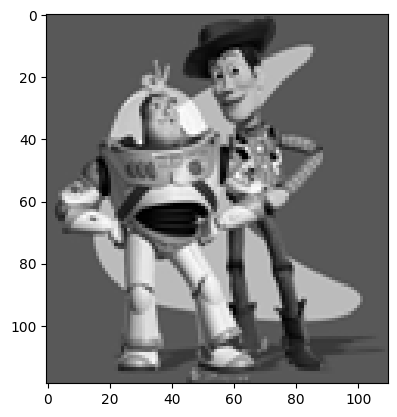
For this part, the objective was to create an image similar to a target image, trying to minimize the sum-of-squared distances between gradients (differences between two adjacent pixels). I used a toy example of Woody and Buzz Lightyear in Gray. The images were very similar. The max error was very low: 0.0010002051356807207.

For this part, I implemented Poisson blending. The purpose was to blend in an object image (masked part) into a background image. For the constraints, I tried to match the gradients between new pixels and their four-neighbors with the source image (masked), so I implemented this as a linear equation. For any pixels on the border of the mask (with neighbors outside the mask), I instead tried to match the gradient between those pixels and the background image's corresponding pixel with the gradient from the source image. The least-squares problem is as displayed below, where v is the new intensity values, s is from the source region, and t is from the target image (background image). N_i is the 4-neighborhood of pixel i, and S is the set of pixels within the mask. The utils functions were very helpful here, the provided functions gave the mask as well as infrastructure for placing the images together.

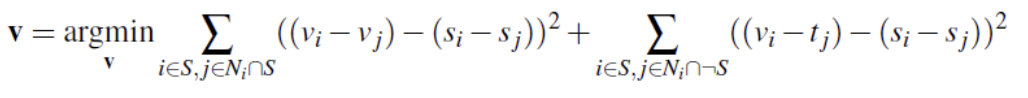
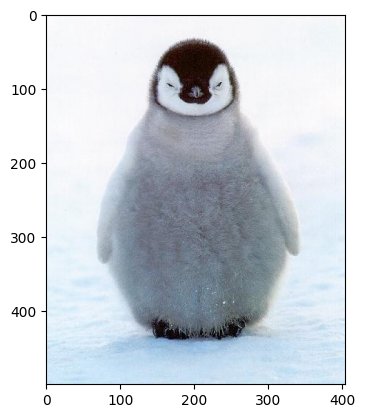
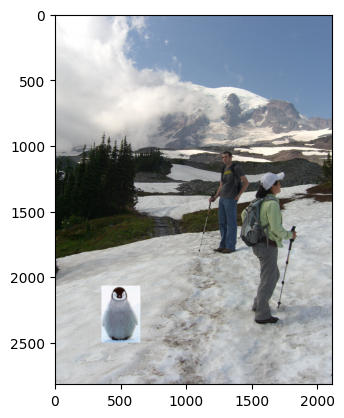
Here, I applied the idea of mixed gradients. Instead of trying to match the gradient between the new pixel and its neighbor with that from the source image, I tried to match it with the gradient from either the source image or the target (background) image, depending on which one had a greater absolute value. Output is displayed. The equation is also displayed, where d_ij is either s_i - s_j or t_i - t_j, depending on which has a larger absolute value.

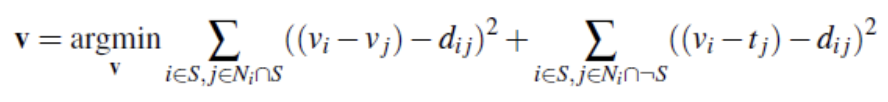
Here, I attempted creating a cartoon-like effect on images. I started by computing the gradients and then using a binary threshold applied to the magnitude for edge enhancement. I used a bilateral filter to smooth the image while preserving edges, helping create the cartoon effect. I also clustered the colors using cv2.kmeans so the basis of colors is smaller. I then blended the created edge mask with the quantized colors image and displayed results below.

In this part, I created images of different focus using the same dataset of 289 images. The idea was that each image is taken from a different camera CoP, and we want to average all of the images with different shifts. With positive shifts, the image would focus more in the foreground, whereas negative shifts would cause the image to appear more focused in the background. For the chessboard dataset, I did this for shifts of magnitude ranging from -1 to 1. My results are displayed below.

For this part, I used varying numbers of images taken around the center image (8, 8). I tried this for the single image, the average of a 3x3 box around it, 5x5, all the way up to 17x17 (entire dataset). I also incorporated the depth refocus (shifting) before averaging to alter the focus. The idea is that averaging more images simulates a narrower aperture, and averaging less images simulates a wider aperture.

Through this project, I learned about how one can artificially change the depth focus with the same images. I read a bit of the paper and learned about the mathematics of how digital refocusing works. I also learned about how to simulate a narrower or wider aperture through this project. This was a very interesting project to implement and the results turned out to be nice!